This proof, at 10 minutes, may be the "bloody marvellous" one Edsger Dijkstra mentioned. The reason I suspect this is that Google seem to have rigged the blog post search on blogger.com to not find "Dijkstra's" or "Banker's". See Teaching Men how to Bank and The Foundation (Part II) which includes a link to Dijkstra's Proof of The Banker's Algorithm.
On the observations at 14 minutes 33 seconds, see:
And on limits of Fibonacci sums at 2 minutes 42 seconds in this video:
Now listen to this description of a Babylonian clay tablet which is thought to be around 3,800 years old. At 11 minutes 49 seconds note how the vertical side of the triangle is unity. Note also the theorem of Euclid which relates the mean proportional of two numbers to the perpendicular height of the right-angled triangle lying in the semi-circle. For some reason, blogger won't let me post this youtube link inline: https://youtu.be/L24GzTaOll0 but here's a snapshot:
Now watch this video and note the connections between decimal and sexagesimal arithmetic which turn up in the Pisano relation, and howLagrange was interested in these when he came to study dynamics and stability of the Solar System.
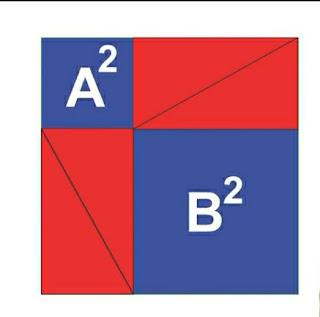
Now note the proof of Pythagoras' at 1 minute 53 seconds which takes 4 copies of a right triangle and rearranges them like this:
And then, see the exercise at 15 minutes 51 seconds which shows this:
Now look at 9 minutes 30 seconds of this video, on the irrationality of the Golden mean:
Now check out theorems about the squares of primes: for example, that they are all of the form 24n+1.
Then look up this 2100 year old Greek calculating machine found in a shipwreck in the early 1900s, ... Note the numbers of teeth on the gears, ... 10 minutes 13 seconds, ... and how they were used to synthesize intervals as portions of one year.
Now look at this way of synthesizing intervals using Fourier series
But it goes on to connect to ideas about uncountability and computability too. For example, check this cute theorem in the N+1=N video at 23 minutes 30 seconds, then listen to Jade on Cantor's proof of the uncountability of the reals
That should give you a bunch of interesting ideas to think about in regard to these questions: John H. Conway on Weird Programming Languages.
To Be Continued, ...
On the observations at 14 minutes 33 seconds, see:
And on limits of Fibonacci sums at 2 minutes 42 seconds in this video:
Now listen to this description of a Babylonian clay tablet which is thought to be around 3,800 years old. At 11 minutes 49 seconds note how the vertical side of the triangle is unity. Note also the theorem of Euclid which relates the mean proportional of two numbers to the perpendicular height of the right-angled triangle lying in the semi-circle. For some reason, blogger won't let me post this youtube link inline: https://youtu.be/L24GzTaOll0 but here's a snapshot:
Now watch this video and note the connections between decimal and sexagesimal arithmetic which turn up in the Pisano relation, and howLagrange was interested in these when he came to study dynamics and stability of the Solar System.
Now note the proof of Pythagoras' at 1 minute 53 seconds which takes 4 copies of a right triangle and rearranges them like this:
And then, see the exercise at 15 minutes 51 seconds which shows this:
Now look at 9 minutes 30 seconds of this video, on the irrationality of the Golden mean:
Now check out theorems about the squares of primes: for example, that they are all of the form 24n+1.
Then look up this 2100 year old Greek calculating machine found in a shipwreck in the early 1900s, ... Note the numbers of teeth on the gears, ... 10 minutes 13 seconds, ... and how they were used to synthesize intervals as portions of one year.
Now look at this way of synthesizing intervals using Fourier series
But it goes on to connect to ideas about uncountability and computability too. For example, check this cute theorem in the N+1=N video at 23 minutes 30 seconds, then listen to Jade on Cantor's proof of the uncountability of the reals
That should give you a bunch of interesting ideas to think about in regard to these questions: John H. Conway on Weird Programming Languages.
To Be Continued, ...


No comments:
Post a Comment